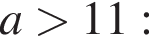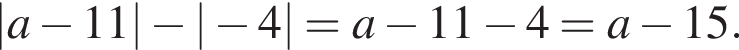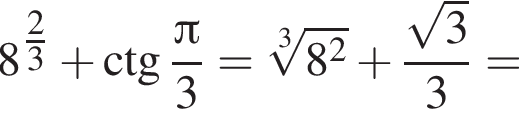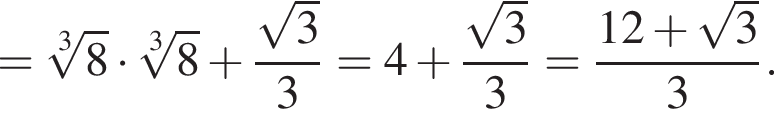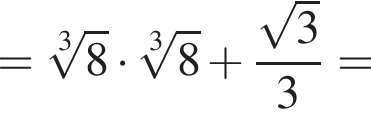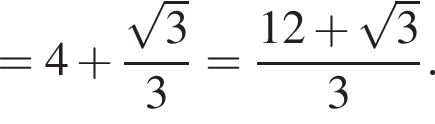Используя данные рисунка, найдите градусную меру угла 1 треугольника АВС.
Треугольник ABC — равнобедренный с основанием AB. Используя данные рисунка, найдите градусную меру угла BAC треугольника ABC.
Запишите (11x)y в виде степени с основанием 11.
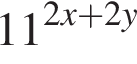
Определите остаток, который получится при делении на 9 числа 83 245.
Если вписанный угол KML изображенный на рисунке, равен 38°, то вписанный угол KNL равен:
На рисунке изображена правильная четырехугольная пирамида. Среди отрезков SB, MQ, SM, SO, MN укажите отрезок, который является апофемой правильной четырехугольной пирамиды.
Прямые a и b, пересекаясь, образуют четыре угла. Известно, что сумма трех углов равна 210°. Найдите градусную меру меньшего угла.
Если MK — диаметр, O — центр окружности,
 (см. рис.), то градусная мера вписанного угла NMK равна:
(см. рис.), то градусная мера вписанного угла NMK равна:
Результат упрощения выражения 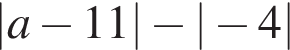 при
при ![]() имеет вид:
имеет вид:
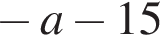
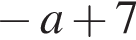
Найдите значение выражения 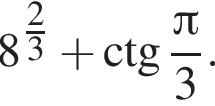
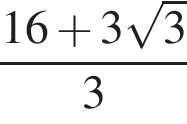
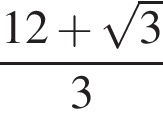
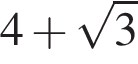
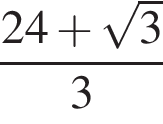


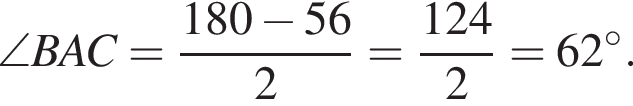
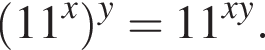
 равна 360°, поэтому четвертый угол равен 150°. Углы 1 и 3, 2 и 4 — вертикальные, следовательно, они равны. Смежные углы в сумме 180°, следовательно, меньший угол равен 30°.
равна 360°, поэтому четвертый угол равен 150°. Углы 1 и 3, 2 и 4 — вертикальные, следовательно, они равны. Смежные углы в сумме 180°, следовательно, меньший угол равен 30°.